x = u² y = v z = w²
de modo a converter o sistema de coordenadas cartesianas em um novo sistema.
Considerando as relações apresentadas, assinale a alternativa que contém o jacobiano associado à essa mudança de coordenadas.
-
a)
J = 4uw.
-
b)
J = 2u.
-
c)
J = 2w.
-
d)
J = 2uw.
-
e)
J = 4uvw.
Para o estudo do momento de inércia de um sólido podemos empregar o cálculo de integrais triplas. Considere um sólido de densidade constante, C, e limitado pelos planos x = ±1, z = ±1, y = 3 e y = 5 . Determine o momento de inércia desse sólido em relação ao eixo z.
Assinale a alternativa correta.
-
a)
0.
-
b)
.
-
c)
.
-
d)
.
-
e)
.
No cálculo de integrais triplas podemos adotar diferentes sistemas de coordenadas que são selecionados de acordo com as características da região de integração, ou mesmo da função a ser integrada. Diante disso, considere a função f(x,y,z) = 1 e que a região G é delimitada por uma semiesfera de raio 1.
Assinale a alternativa que contém o valor da integral da função f(x,y,z) sobre a região G.
-
a)
.
-
b)
1.
-
c)
.
-
d)
.
-
e)
.
Para calcular a integral de linha da função sobre a curva C
definida como o segmento de reta que une os pontos A(-1,0) e B(3,1), é
necessário, inicialmente, construir uma parametrização para C.
A partir dessas informações, assinale a alternativa que associa corretamente a integral de linha com a integral definida que pode ser empregada em seu cálculo.
-
a)
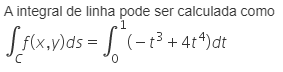
-
b)
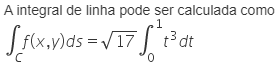
-
c)
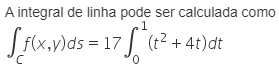
-
d)
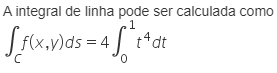
-
e)
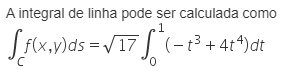
Considere que um pedaço de arame esteja disposto no espaço de tal forma que assume o formato de uma curva C com a seguinte parametrização:
para 0 = t = 2. Se desejamos determinar a massa desse arame podemos empregar o cálculo das integrais de linha sobre C, porém, para isso, precisamos conhecer a função densidade correspondente.
Se a função densidade associada a esse arame é da forma
qual é a massa total, em gramas, do arame descrito?
Assinale a alternativa correta.
-
a)
5 g.
-
b)
7,5 g.
-
c)
15 g.
-
d)
21 g.
-
e)
25 g.
