AV1 - CÁLCULO DIFERENCIAL E INTEGRAL 2 [RESOLVIDA]

1) O nome Teorema Fundamental do Cálculo é apropriado, pois ele estabelece uma conexão entre os dois ramos do cálculo: o cálculo diferencial e o cálculo integral. O cálculo diferencial surgiu do problema da tangente, enquanto o cálculo integral surgiu de um problema aparentemente não relacionado, o problema da área. O mentor de Newton em Cambridge, Isaac Barrow (1630-1677), descobriu que esses dois problemas estão, na verdade, estreitamente relacionados. Ele percebeu que a derivação e a integração são processos inversos. O Teorema Fundamental do Cálculo dá a relação inversa precisa entre a derivada e a integral. Foram Newton e Leibniz que exploraram essa relação e usaram-na para desenvolver o cálculo como um método matemático sistemático. Em particular, eles viram que o Teorema Fundamental os capacitava a calcular áreas e integrais muito mais facilmente, sem que fosse necessário calculá-las como limites de somas.

Considerando o contexto apresentado e seu conhecimento introdutório sobre integrais assinale a alternativa correta na qual apresenta resumidamente uma passo a passo para a solução da integral ..

---

Alternativas:

• a)

  

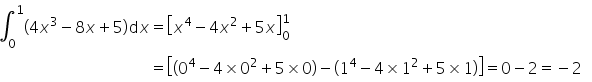
• b)

  

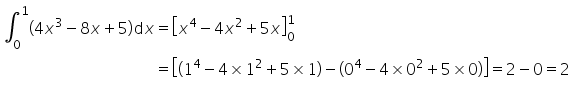
• c)

  

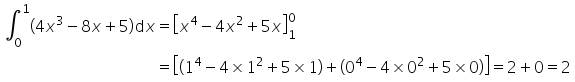
• d)

  

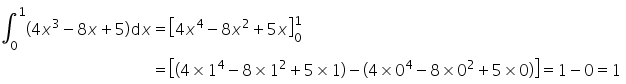
• e)

  

2)

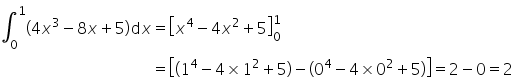
Para convertermos um ponto P=(x,y) do plano cartesiano para coordenadas polares precisamos ter em mente que: "para cada ponto P do plano, são associadas coordenadas (¿,¿) descritas da seguinte forma:

- ¿ é a distância do polo O ao ponto P

- ¿ é o ângulo entre o eixo polar e o seguimento de reta ."

 

Para auxiliar nessa visualização, observe o gráfico a seguir:

Fonte: Elaborada pela autora

Diante dessa informação e dos conteúdos da unidade, converta a reta y=-2 em coordenadas polares e assinale a alternativa que descreve esse resultado.

---

Alternativas:

• a)

   

• b)

   

• c)

   

• d)

   

• e)

  

3)

O cálculo do comprimento de uma curva é uma das informações importantes que usamos para avaliar a área dessa curva.

Seja em coordenadas cartesianas

ou em coordenadas polares

o comprimento de um arco é calculado utilizando integrais definidas.

 Calcule o comprimento do da circunferência descrita pela equação .

---

Alternativas:

• a)

  8p

• b)

  2p

• c)

  4p

• d)

  16p

• e)

  3p

4)

Um dos grandes avanços da geometria clássica foi a obtenção de fórmulas para determinar a área e o volume de triângulos, esferas e cones. Contudo há um método para calcular áreas e volumes das formas mais gerais. Esse método, chamado integração, é uma ferramenta para calcular muito mais do que áreas e volumes. A integral é de fundamental importância em estatística, ciências e engenharia. Ela nos permite calcular quantidades que vão desde probabilidades e médias até consumo de energia e forças que atuam contra as comportas de uma represa. Estudaremos uma variedade dessas aplicações no próximo capítulo, mas, neste, iremos nos concentrar no conceito de integral e em seu uso no cálculo de áreas de várias regiões com contornos curvos.

 

Tendo como referência seu conhecimento as integrais e sua relação com áreas de curvas, julgue as afirmações abaixo em (V) Verdadeiras ou (F).

( ) A integral  pode ser utilizada para calcular a área da região delimitada pela função contínua , pelas retas verticais  e  e pelo eixo .  

( ) A área delimitada superiormente pela curva , inferiormente pela curva  e delimitado pelas retas   e    pode ser calculada por .

( ) A única aplicação para as integrais em engenharia são os cálculos de área abaixo de uma curva e entre duas curvas. Além disso, a integral se restringe a uma ferramenta matemática pouco útil.

( ) Ao calcular a integral  de uma função contínua estamos calculando um valor que representa o comprimento total do arco dessa curva de   até  .  

Assinale a alternativa que apresenta a sequência correta.

---

Alternativas:

• a)

  F – V – V – V

• b)

  V – F – V – F

• c)

  V – V – F – V

• d)

  V – V – F – F

• e)

  F – V – V – F

5)

É muito frequente, em se tratando de modelar um fenômeno ou um experimento qualquer, obtermos equações que envolvam as “variações” das quantidades (variáveis) presentes e consideradas essenciais. Desta forma, as leis que regem tal fenômeno são traduzidas por equações de variações. Quando estas variações são instantâneas, o fenômeno se desenvolve continuamente e as equações matemáticas são de­ nominadas equações diferenciais, ao passo que se as variáveis envolvidas forem discretizadas, isto é, funções de uma rede de pontos, em que temos as médias das variações, então as equações que descrevem o fenômeno serão denominadas equações de diferenças.

 

Tendo como referência seu conhecimento sobre Equações Diferenciais Ordinárias (EDO) Separáveis, julgue as afirmações abaixo em (V) Verdadeira ou (F) Falsa.

( ) A EDO   é separável, e pode ser escrita como .

( ) A EDO   é separável, e pode ser escrita como  .

( ) A EDO  é separável, e pode ser escrita como .

( ) A EDO   é separável, e pode ser escrita como .

Assinale a alternativa que apresenta a sequência correta.

---

Alternativas:

• a)

  F – V – V – V

• b)

  V – F – V – F

• c)

  V – V – F – V

• d)

  F – F – V – V

• e)

  F – V – V – F

 

 ATIVIDADE RESOLVIDA

 

R$15,00 NO PIX

eng.carlosjfilho@hotmail.com

APÓS FAZER O PIX ACESSE O LINK ABAIXO 
Contatos

AP1 Estruturas de Concreto Armado II: Projeto de Escada

O primeiro passo para o dimensionamento de uma escada é verificar se as características geométricas da escada estão adequadas de acordo com NBR 9050:2004.

As dimensões dos pisos e espelhos devem ser constantes em toda a escada, atendendo às condições estabelecidas em projeto.

 

Figura 1: Exemplo prático das características geométricas de uma escada.

 

Pelo projeto da figura 1, o maior vão (S2), é o trecho intermediário da escada, onde passará o corte BB, sendo assim necessário verificar as espessuras da escada, que irá compor os lances (AA), (BB) e (CC). Podemos assim verificar que a escada será composto por três lajes, que estarão passando pelos cortes (AA), (BB) e (CC). Cada lance da escada ira ter uma espessura de início de projeto, que posteriormente será verificado.

Podemos observar na figura 2 que o posicionamento das vigas (V1; V2; V3; V4) é estratégico, pois as vigas no projeto serão elementos de apoio para as lajes (lances). Pode-se ainda compreender que as lajes servem de apoio, condição a qual tem que ser verificado em projeto.  

Com os valores totais de carregamento verificados e calculados (carga permanente e acidental), o próximo passo é montar o modelo estrutural da escada, ou seja, compreender que:

• Laje L1 se apoia na viga V1 e na viga V2 (figura 3).

Figura 3: Armaduras principais do lance (L1) apoiadas nas vigas (V1 e V2). 

• Laje L2 se apoia na viga V3 e na laje L1 (figura 4).

Figura 4: Armaduras principais do lance da laje (L2) apoiadas na viga (V3) e no lance da laje (L1).

• Laje L3 se apoia na viga V4 e laje L2 (figura 5).

Figura 5: Armaduras principais do lance da laje (L3) apoiadas na viga (V4) e no lance da laje (L2).

De acordo com as informações e com tudo que foi aprendido até aqui, responda aos seguintes questionamentos:

 

1. Explique porque as amaduras principais presente na laje (L2) são posicionadas na parte de cima da laje (L1).

 

2. Identifique, no modelo estrutural, o sentido correto de início de dimensionamento da escada, sabendo que as lajes, possuem um sentido correto de posicionamento, ou seja:

• Laje L1 se apoia na viga V1 e na viga V2.
• Laje L2 se apoia na viga V3 e na laje L1.
• Laje L3 se apoia na viga V4 e laje L2.

 

3. Explique o conceito presente no detalhamento executado nas figuras 3 e 4, representada na figura 6.

 

 ATIVIDADE RESOLVIDA

 

R$30,00 NO PIX

eng.carlosjfilho@hotmail.com

APÓS FAZER O PIX ACESSE O LINK ABAIXO 
Contatos

AP1 OBRAS DE TERRA RESOLVIDA [COM FEEDBACK POSITIVO]

Tratando-se de Compactação, analise a situação e responda ao questionamento:

Quantas passadas de um compactador tipo ‘’Rolo Pé de Carneiro” serão necessárias em uma camada de compactação com 0,30 m de espessura?

Considerar que irá desenvolver uma energia de compactação igual à do ensaio Proctor Normal [soquete de 4,5 kg] em cada camada e o equipamento de compactação rolo pé de carneiro tem as seguintes características: 

• peso= 115,0kg; 
• altura de queda= 0,50m
• Φ= 0,34m

Informações:

n= 1 a 30 cm [número de camadas e espessura].

H= altura da camada de solo a ser compactada: 30cm.

 

 ATIVIDADE RESOLVIDA

 

R$30,00 CHAVE PIX pixblog@mail.com

APÓS FAZER O PIX ACESSE O LINK ABAIXO 
Contatos

Sistemas Estruturais - Atividade Prática de Aprendizagem 2

Pergunta 1 De acordo com o exposto pela ABNT NBR 6118 (2003), nos projetos das estruturas correntes, a agressividade ambiental deve ser classificada de acordo com o apresentado no Quadro I e pode ser avaliada, simplificadamente, segundo as condições de exposição da estrutura ou de suas partes. 

Quadro I - Classes de agressividade ambiental

 

 Tendo como referências as informações acima, é correto afirmar que a agressividade do meio ambiental nas estruturas de concreto ou de suas partes está relacionada:
  Somente às ações físicas que atuam sobre as estruturas de concreto, independentemente das ações mecânicas, das variações volumétricas de origem térmica, da retração hidráulica e de outras previstas no dimensionamento das estruturas de concreto.
  Somente às ações químicas que atuam sobre as estruturas de concreto, independentemente das ações mecânicas, das variações volumétricas de origem térmica, da retração hidráulica e de outras previstas no dimensionamento das estruturas de concreto.
  Somente às ações mecânicas, às variações volumétricas de origem térmica, à retração hidráulica e outras previstas no dimensionamento das estruturas de concreto.
  Às ações físicas e químicas que atuam sobre as estruturas de concreto, dependendo das ações mecânicas, das variações volumétricas de origem térmica, da retração hidráulica e de outras previstas no dimensionamento das estruturas de concreto.
  Às ações físicas e químicas que atuam sobre as estruturas de concreto, independentemente das ações mecânicas, das variações volumétricas de origem térmica, da retração hidráulica e de outras previstas no dimensionamento das estruturas de concreto.
 
Pergunta 2 Leia o trecho abaixo e responda:

No método das forças é realizado com um sistema de forças que nos geram as equações necessárias para resolver o nosso esquema estático. O método dos deslocamentos deve ser trabalhado com um sistema de deslocamentos para conseguir essas informações.

Explique com suas palavras o que é engastamento perfeito.
 

 

 ATIVIDADE RESOLVIDA

 

 R$15,00

Contatos

ATIVIDADE 4 - CÁLCULO DIFERENCIAL E INTEGRAL I - 54/2023

Se uma função f for derivável, então f ’ é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f ’ existir, então ela será chamada derivada segunda de f (ou de ordem 2), e assim por diante. As derivadas primeira e segunda de uma função carregam informações importantes, como: seja f uma função contínua no intervalo
a, b e derivável em (a, b).

i) Se f ’(x) > 0 para todo x ∈ (a, b), então f é crescente em a, b.
ii) Se f ’(x) < 0 para todo x ∈ (a, b), então f é decrescente em a, b. 

Agora: Seja f uma função derivável em um intervalo (a, b) e seja c um ponto crítico de f neste intervalo, isto é, f ’(c)= 0, com a < c < b. Se f admite a derivada segunda em (a, b) então:
i) Se f ”(c) < 0, f tem um valor máximo relativo em c.
ii) Se f ”(c) > 0, f tem um valor mínimo relativo em c.

Sobre as aplicações das derivadas primeira e segunda para obter possíveis pontos de mínimo ou máximo de uma função, observe a função a seguir: f(x) = -x + 15.x . Ao estudar a disciplina de Cálculo, Matheus se depara com tal função e precisa saber, caso exista, qual ou quais são os pontos de mínimo e/ou de máximo dessa função f(x). Ao fazer os cálculos usando a derivada primeira e a derivada segunda da função f(x), Matheus poderá encontrar os pontos de mínimo e/ou de máximo. Caso Matheus os encontre, tais valores serão:
0.
10.
15.
0 e 10.
10 e 15.

A aparência externa remete à borracha. Ninguém imagina, no entanto, que o pneu possa contar com tantos e variados componentes responsáveis pelo desempenho necessário para garantir, com segurança, todas as características exigidas por esse complexo produto. Ele é fabricado para rodar por milhares de quilômetros
em todos os tipos de estrada, em terrenos enlameados, pistas pedregosas, desertos e até terras geladas. A proporção dos itens na composição do pneu varia de acordo com seu uso. Por exemplo, nos pneus de automóveis de passeio, que rodam em estradas pavimentadas, a borracha sintética é mais usada que a borracha natural. Nos pneus de caminhões de carga, empregados em múltiplas estradas, predomina o uso da borracha natural, por sua maior resistência aos cortes e lacerações. A presença do negro de fumo ou carbono amorfo, derivado do petróleo, é fundamental em todos os compostos de borracha, porque confere resistência à abrasão e deixa o pneu preto. Além disso, é imprescindível o uso do enxofre, elemento vulcanizante, somado com vários outros produtos químicos, catalisadores, plastificantes e cargas
reforçantes. Com relação à fabricação de pneus, a função R(q) = -0,4q +400q expressa a receita R em reais, para a venda de q unidades de um tipo de pneu. Com base na função dada, assinale a alternativa que expressa, respectivamente, a quantidade de pneus vendidos para se ter a receita máxima e o valor da receita máxima:
Quantidade q = 100 e receita R$ 1000,00.
Quantidade q = 100 e receita R$ 10.000,00.
Quantidade q = 500 e receita R$ 10.000,00.
Quantidade q = 500 e receita R$ 100.000,00.
Quantidade q = 100 e receita R$ 1000.000,00.

Uma integral é dita indefinida quando não se conhece os limites de integração, ou seja, o intervalo no qual ela está sendo integrada. Exemplo: . Na integração indefinida, a função resultante será a função integrada F(x), sendo necessário somá-la a uma constante, chamada de constante de integração. Diferentemente da integral indefinida, os limites da integral definida já estão estabelecidos. Para resolvê-la, basta encontrar a integral da função em questão, e neste resultado substituir os valores dos limites superior e inferior. Como as constantes de integração são iguais, a integral definida é a subtração das funções primitivas substituídas pelos limites superior e inferior, neste caso (B e A, respectivamente). Com relação às definições sobre Integral Definida, observe a função a seguir: f(x)= 5x +7x-2. Calculando a Integral Definida dessa função em relação à variável x, nos valores 0 e 2, ou seja, teremos como resultado:
0.
-4.
10.
14.
23.

Uma das aplicações da Integral de uma função f ‘(x) é obter a função primitiva f(x) quando se tem a derivada, ou seja, f ‘(x). Ao fazer um trabalho em uma empresa, João sabe que a taxa de variação instantânea, a derivada, da função receita de um produto é dada pela função R ‘(q) = 3q , em que R representa a receita em reais, e q representa a quantidade de produtos vendidos em unidades. João precisa saber qual é o valor da receita quando se vende 500 unidades de tal produto. Assim, João faz a Integral da função R ‘(q) obtendo a função R(q) e a calcula no valor 500. Sobre o valor que João encontra após esses cálculos, assinale a alternativa correta:
500 + c.
125000 + c.
250000 + c.
500000 + c.
125000000 + c.

Como estudado na disciplina de cálculo, é possível determinar extremos, assim como os mínimos e/ou máximos de uma função utilizando as suas derivadas. Esses recursos podem ser úteis para se encontrar soluções de problemas que exigem os melhores valores possíveis de uma variável, e muito aplicáveis no cotidiano em problemas de otimização, otimização que é fundamental em qualquer meio aplicado afim de se descobrir mínimos ou máximos do que se está estudando ou trabalhando. Sobre a questão de mínimos e/ou máximos de funções, observe o gráfico a seguir. No gráfico, consta informações sobre mínimos e máximos de uma função. Sobre as representações expressas no gráfico, analise as afirmativas a seguir.
I. O maior valor da função f(x) acontece quando ela é aplicada no ponto f.
II. Sendo f(x) a função com o gráfico representado acima, a derivada segunda de f(x) calculada no ponto b, apresenta um valor positivo.
III. Sendo f(x) a função com o gráfico representado acima, a derivada segunda de f(x) calculada no ponto c, apresenta um valor positivo.
IV. Sendo f(x) a função com o gráfico representado acima, a derivada primeira de f(x), é igual a zero no ponto d.
V. O menor valor da função f(x) acontece quando ela é aplicada no ponto c.
É correto o que se afirma em:
I, apenas.
I e II, apenas.
II, III e IV, apenas.
IV e V, apenas.
I, III, IV e V, apenas

 

 ATIVIDADE RESOLVIDA

 

R$12,00 NO PIX

eng.carlosjfilho@hotmail.com  R$15,00 NO CARTÃO DE CRÉDITO

Contatos