1) A habilidade de resolver EDOs é altamente valorizada no mercado de trabalho. Profissionais que dominam essa área são frequentemente procurados por empresas de tecnologia, pesquisa científica, consultorias e indústrias que necessitam de modelagem matemática e análise de dados. Diante deste contexto, analise as afirmativas a seguir:
I - A capacidade de aplicar métodos analíticos e numéricos para resolver EDOs amplia as oportunidades de carreira, permitindo que o profissional se destaque em projetos de inovação e desenvolvimento.
II - A compreensão das estratégias de resolução, como métodos de separação de variáveis, transformadas de Laplace, e técnicas numéricas como o método de Euler e Runge-Kutta, é crucial.
III - A competência em EDOs só limita o enriquecimento do conhecimento técnico do profissional, e não abre portas para uma vasta gama de oportunidades profissionais, o que não torna-o um recurso valioso.
Marque a alternativa correta.
Alternativas:
- a)
Apenas I e II estão corretas.
- b)
Apenas I e III estão corretas.
- c)
Apenas II e III estão corretas.
- d)
Apenas I está correta.
- e)
Apenas III está correta.
Equações diferenciais ordinárias podem ser empregadas na representação de determinados fenômenos. Devido a esse fato, é fundamental o estudo dos métodos que podem ser empregados na resolução destes problemas, de acordo com as classificações das equações.
Seja a equação diferencial ordinária dada por
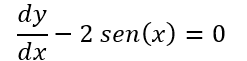
Considerando suas principais características, qual a classificação da equação em questão quanto ao grau e linearidade? Marque a alternativa correta.
Alternativas:
- a)
Equação diferencial linear de 1ª ordem
- b)
Equação diferencial não linear de 1ª ordem
- c)
Equação diferencial linear de 2ª ordem
- d)
Equação diferencial não linear de 2ª ordem
- e)
Equação diferencial linear de 3ª ordem
Considere os itens C1, C2, C3, I, II e III.
C1: Equação diferencial ordinária não linear de 2ª ordem
C2: Equação diferencial ordinária linear de 2ª ordem
C3: Equação diferencial ordinária linear de 1ª ordem
Associe as equações diferenciais (denotadas por I, II e III) com as respectivas classificações (indicadas por C1, C2 e C3) nas quais os mesmos podem ser incluídos.
Assinale a alternativa que indica todas as associações corretamente:
Alternativas:
- a)
I – C1; II – C3; III – C2.
- b)
I – C3; II – C1; III – C2.
- c)
I – C2; II – C3; III – C1.
- d)
I – C3; II – C2; III – C1.
- e)
I – C1; II – C2; III – C3.
A partir dos cálculos de integrais, analise as afirmações apresentadas no que segue e a relação proposta entre elas:
I. As integrais triplas podem ser empregadas no cálculo do volume segundo os sistemas de coordenadas cartesianas, cilíndricas e esféricas.
PORQUE
II. A integral tripla da função f(x, y, z) = 2xyz com limites de integração fornecidos a partir de S, fornece o volume de S no espaço.
Com base nessas informações, assinale a alternativa correta:
Alternativas:
- a)
As afirmações I e II estão corretas, e a II é uma justificativa correta da I.
- b)
As afirmações I e II estão corretas, mas a II não é uma justificativa correta da I.
- c)
A afirmação I está incorreta, enquanto que a II está correta.
- d)
A afirmação I está correta, enquanto que a II está incorreta.
- e)
As afirmações I e II estão incorretas.
Analise a equação diferencial ordinária dada por
y’’+ 2y’ – 15y = 0
Com base nas informações apresentadas, assinale a alternativa que indica corretamente quais são as raízes da equação característica associada à equação diferencial ordinária apresentada:
Alternativas:
- a)
r1 = 5 e r2 = -3.
- b)
r1 = 2 e r2 = 1.
- c)
r1 = 3 e r2 = -5.
- d)
r1 = -1 e r2 = 0.
- e)
r1 = -2 e r2 = 3.











Nenhum comentário:
Postar um comentário
Dúvidas? Sugestões? Fale com o Professor Carlão!