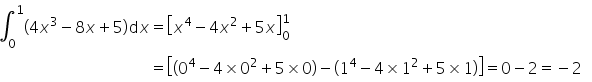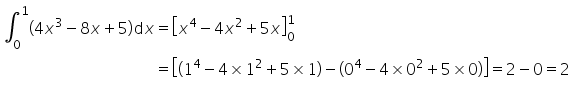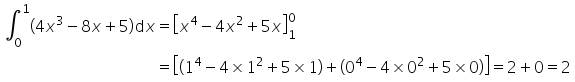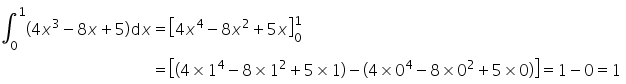AV2 - Cálculo Diferencial e Integral 2 [RESOLVIDA]

1) As integrais duplas fazem parte dos conceitos fundamentais de Cálculo Diferencial e Integral quando estamos interessados em trabalhar com noções espaciais de volumes ou, até mesmo áreas de superfícies. Com base nesse conceito, julgue as informações a seguir:

 

I. Para o cálculo de uma integral dupla em uma região retangular, procedemos com o uso de dodecaedros para a aproximação do volume de uma superfície.

II. O vetor gradiente é utilizado para o cálculo de integrais iteradas.

III. O volume da superfície é aproximado pelo limite da soma de Riemann para funções de duas variáveis.

É correto o que se afirma em:

---

Alternativas:

• a)

  I, apenas.

• b)

  II, apenas.

• c)

  III, apenas.

• d)

  I e III, apenas.

• e)

  II e III, apenas.

2)

Podemos aplicar o vetor gradiente em diversas situações, uma delas é encontrar o valor do vetor gradiente em um ponto de uma superfície. Pensando nesse conceito, qual seria o valor do vetor gradiente no ponto descrito pelas coordenadas (-2, 1, -3) do elipsoide de equação descrita ?

Assinale a alternativa correta.

---

Alternativas:

• a)

  

• b)

  

• c)

  

• d)

  

• e)

  

3)

Suponha que em uma empresa de caixas de papelão são fabricados três tamanhos diferentes, pequena, média e grande. O custo para fabricação de uma caixa pequena é de R$ 1,50, de uma caixa média é de R$2,50 e de uma caixa grande é de R$4,00. O custo fixo da empresa é de R$ 5500,00. Com base nessa situação, analise os itens que seguem.

I. O problema tem duas variáveis: a quantidade de caixas produzidas, que pode ser denotado por x e o custo total da produção que pode ser denotado por C(x).

II. O problema tem como variáveis dependentes a quantidade de caixas médias produzidas, a quantidade de caixas pequenas produzidas e o custo fixo e como variável independente o custo de produção.

III. O problema tem como variável dependente o custo de produção e como variáveis independentes a quantidade produzida de caixas pequenas, a quantidade produzida de caixas média e a quantidade produzida de caixas grandes.

Assinale a alternativa correta.

---

Alternativas:

• a)

  Apenas o item I está correto.

• b)

  Apenas o item II está correto.

• c)

  Apenas o item III está correto.

• d)

  Apenas os itens I e II estão corretos.

• e)

  Apenas os itens I e III estão corretos.

4)

 Uma função f de duas variáveis é uma regra que associa a cada par ordenado de números reais (x, y)  de um conjunto D um único valor real, denotado por f(x, y).O conjunto D é denominado domínio de f e sua imagem é o conjunto de valores possíveis de f .

Com base nessas informações, analise a função

Assinale a alternativa que contém o domínio da função.

---

Alternativas:

• a)

   

• b)

   

• c)

   

• d)

   

• e)

   

5)

Se T(x,y) for a temperatura em um ponto (x,y) sobre uma placa delgada de metal no plano , então as curvas de nível de T são chamadas de curvas isotérmicas. Todos os pontos sobre tal curva têm a mesma temperatura. Suponha que uma placa ocupa o primeiro quadrante e T(x,y) = x + y.Com base nessas afirmações, analise os itens que seguem.

I. Quando T = 1 temos uma curva de nível cujo esboço é uma reta.

II. O domínio da função T(x,y) é .

III. Uma formiga, inicialmente em (1, 4), anda sobre a placa de modo que a temperatura ao longo de sua trajetória permanece constante, logo podemos afirmar que a temperatura ao longo de sua trajetória é 5.

Assinale a alternativa correta.

---

Alternativas:

• a)

  Apenas o item I está correto.

• b)

  Apenas os itens I e III estão corretos.

• c)

  Apenas os itens I e II estão corretos.

• d)

  Apenas os itens II e III estão corretos.

• e)

  Os itens I, II e III estão corretos.

 

 ATIVIDADE RESOLVIDA

 

R$15,00 NO PIX

eng.carlosjfilho@hotmail.com

APÓS FAZER O PIX ACESSE O LINK ABAIXO 
Contatos

AV1 - CÁLCULO DIFERENCIAL E INTEGRAL 2 [RESOLVIDA]

1) O nome Teorema Fundamental do Cálculo é apropriado, pois ele estabelece uma conexão entre os dois ramos do cálculo: o cálculo diferencial e o cálculo integral. O cálculo diferencial surgiu do problema da tangente, enquanto o cálculo integral surgiu de um problema aparentemente não relacionado, o problema da área. O mentor de Newton em Cambridge, Isaac Barrow (1630-1677), descobriu que esses dois problemas estão, na verdade, estreitamente relacionados. Ele percebeu que a derivação e a integração são processos inversos. O Teorema Fundamental do Cálculo dá a relação inversa precisa entre a derivada e a integral. Foram Newton e Leibniz que exploraram essa relação e usaram-na para desenvolver o cálculo como um método matemático sistemático. Em particular, eles viram que o Teorema Fundamental os capacitava a calcular áreas e integrais muito mais facilmente, sem que fosse necessário calculá-las como limites de somas.

Considerando o contexto apresentado e seu conhecimento introdutório sobre integrais assinale a alternativa correta na qual apresenta resumidamente uma passo a passo para a solução da integral ..

---

Alternativas:

• a)

  

• b)

  

• c)

  

• d)

  

• e)

  

2)

Para convertermos um ponto P=(x,y) do plano cartesiano para coordenadas polares precisamos ter em mente que: "para cada ponto P do plano, são associadas coordenadas (¿,¿) descritas da seguinte forma:

- ¿ é a distância do polo O ao ponto P

- ¿ é o ângulo entre o eixo polar e o seguimento de reta ."

 

Para auxiliar nessa visualização, observe o gráfico a seguir:

Fonte: Elaborada pela autora

Diante dessa informação e dos conteúdos da unidade, converta a reta y=-2 em coordenadas polares e assinale a alternativa que descreve esse resultado.

---

Alternativas:

• a)

   

• b)

   

• c)

   

• d)

   

• e)

  

3)

O cálculo do comprimento de uma curva é uma das informações importantes que usamos para avaliar a área dessa curva.

Seja em coordenadas cartesianas

ou em coordenadas polares

o comprimento de um arco é calculado utilizando integrais definidas.

 Calcule o comprimento do da circunferência descrita pela equação .

---

Alternativas:

• a)

  8p

• b)

  2p

• c)

  4p

• d)

  16p

• e)

  3p

4)

Um dos grandes avanços da geometria clássica foi a obtenção de fórmulas para determinar a área e o volume de triângulos, esferas e cones. Contudo há um método para calcular áreas e volumes das formas mais gerais. Esse método, chamado integração, é uma ferramenta para calcular muito mais do que áreas e volumes. A integral é de fundamental importância em estatística, ciências e engenharia. Ela nos permite calcular quantidades que vão desde probabilidades e médias até consumo de energia e forças que atuam contra as comportas de uma represa. Estudaremos uma variedade dessas aplicações no próximo capítulo, mas, neste, iremos nos concentrar no conceito de integral e em seu uso no cálculo de áreas de várias regiões com contornos curvos.

 

Tendo como referência seu conhecimento as integrais e sua relação com áreas de curvas, julgue as afirmações abaixo em (V) Verdadeiras ou (F).

( ) A integral  pode ser utilizada para calcular a área da região delimitada pela função contínua , pelas retas verticais  e  e pelo eixo .  

( ) A área delimitada superiormente pela curva , inferiormente pela curva  e delimitado pelas retas   e    pode ser calculada por .

( ) A única aplicação para as integrais em engenharia são os cálculos de área abaixo de uma curva e entre duas curvas. Além disso, a integral se restringe a uma ferramenta matemática pouco útil.

( ) Ao calcular a integral  de uma função contínua estamos calculando um valor que representa o comprimento total do arco dessa curva de   até  .  

Assinale a alternativa que apresenta a sequência correta.

---

Alternativas:

• a)

  F – V – V – V

• b)

  V – F – V – F

• c)

  V – V – F – V

• d)

  V – V – F – F

• e)

  F – V – V – F

5)

É muito frequente, em se tratando de modelar um fenômeno ou um experimento qualquer, obtermos equações que envolvam as “variações” das quantidades (variáveis) presentes e consideradas essenciais. Desta forma, as leis que regem tal fenômeno são traduzidas por equações de variações. Quando estas variações são instantâneas, o fenômeno se desenvolve continuamente e as equações matemáticas são de­ nominadas equações diferenciais, ao passo que se as variáveis envolvidas forem discretizadas, isto é, funções de uma rede de pontos, em que temos as médias das variações, então as equações que descrevem o fenômeno serão denominadas equações de diferenças.

 

Tendo como referência seu conhecimento sobre Equações Diferenciais Ordinárias (EDO) Separáveis, julgue as afirmações abaixo em (V) Verdadeira ou (F) Falsa.

( ) A EDO   é separável, e pode ser escrita como .

( ) A EDO   é separável, e pode ser escrita como  .

( ) A EDO  é separável, e pode ser escrita como .

( ) A EDO   é separável, e pode ser escrita como .

Assinale a alternativa que apresenta a sequência correta.

---

Alternativas:

• a)

  F – V – V – V

• b)

  V – F – V – F

• c)

  V – V – F – V

• d)

  F – F – V – V

• e)

  F – V – V – F

 

 ATIVIDADE RESOLVIDA

 

R$15,00 NO PIX

eng.carlosjfilho@hotmail.com

APÓS FAZER O PIX ACESSE O LINK ABAIXO 
Contatos