1) Pela regra da substituição, também chamada de regra da cadeia para integrais, temos que se g'(x) for uma função contínua em um intervalo [a,b] conhecido e f(x) for contínua na imagem de u=g(x) então teremos que:
Usando a regra da substituição, assinale a alternativa correta a respeito da igualdade:
a) Não está correta, pois os limites de integração são diferentes.
b) Não está correta, pois o integrando é diferente.
c) Não está correta, pois o resultado de cada uma das integrais apresentadas será diferente.
d) Está correta
e) Nenhuma das alternativas descritas
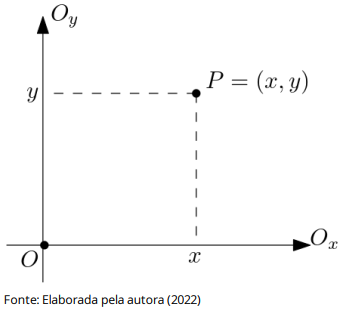
2) Sistemas de coordenadas cartesianas ortogonais bidimensionais são aqueles onde cada ponto está representado nas coordenadas (x,y), onde x determina a distância horizontal deslocada por esse ponto e y determina a distância vertical deslocada por esse ponto, ambas em relação a origem dos sistemas, que se dá pela intersecção dos eixos Ox e Oy descrito por retas perpendiculares, conforme figura a seguir:
Em um sistema de coordenadas polares, cada ponto é descrito por um par de coordenadas da forma (¿,¿), onde ¿ é o raio de uma circunferência gerada pela rotação de ¿, no sentido anti-horário, com centro (a,b) conhecido e ¿ é o ângulo entre o eixo polar e a reta que passa por ¿, conforme pode ser observado na figura a seguir:
3) Você já está familiarizado com operações inversas. Adição e subtração, multiplicação e divisão são operações inversas, bem como potenciação e radiciação. A derivada também tem uma operação inversa, conhecida como antiderivada ou integral. [...] A integração pode ser obtida de forma imediata conhecendo aspectos específicos das funções na qual a operação de integração está sendo aplicada. Com base no que foi estudado sobre as integrais imediatas, analise as afirmativas a seguir:
I. A integral é uma integral exponencial.
II. A integral é uma integral trigonométrica
III. A integral é uma integral polinomial.
IV. A integral é uma integral polinomial.
Considerando o contexto apresentado, é correto o que se afirmar em:
a) Apenas I e II estão corretas.
b) Apenas I e III estão corretas.
c) Apenas I, II e III estão corretas.
d) Apenas II, III e IV estão corretas.
e) I, II, III e IV estão corretas
4) Muitas civilizações primitivas conheciam as fórmulas para a área de polígonos como quadrados, retângulos, triângulos e trapézios. Contudo, os matemáticos primitivos se deparavam com muitas dificuldades para encontrar fórmulas para a área de regiões com contornos curvilíneos, das quais o círculo é o exemplo mais simples. O primeiro progresso real no trato com o problema geral da área foi obtido pelo matemático grego Arquimedes, que obteve áreas de regiões delimitadas por arcos de círculos, parábolas, espirais e vários outros tipos de curvas, usando um procedimento genial mais tarde denominado método de exaustão. [...] O cálculo de áreas pelo método de exaustão era um procedimento muito complicado. Acabou ficando para Matemáticos modernos a descoberta de um método geral de obtenção de áreas que utilizasse explicitamente a noção de limite. Com base no que foi estudado sobre integrais e cálculo de áreas, analise as afirmativas a seguir:
I. O método de Riemann é utilizado para aproximar a área abaixo de uma curva. Esse método consiste basicamente em dividir a região em diversos retângulos e somar a área desses retângulos.
II. A integração é considerada a operação inversa da derivação. De forma geral, chamamos a integral de integral indefinida, onde
III. A integral é uma operação matemática utilizada para determinar áreas. Dessa forma, para resolver uma integral qualquer devemos utilizar as fórmulas de áreas de polígonos.
IV. A integral é um integral polinomial e a integral é uma integral trigonométrica.
Considerando o contexto apresentado, é correto o que se afirma em:
a) Apenas I e II estão corretas.
b) Apenas I e III estão corretas.
c) Apenas I, II e III estão corretas.
d) Apenas I, II e IV estão corretas.
e) I, II, III e IV estão corretas.
5) Sabemos que o cálculo diferencial surgiu do problema da tangente, enquanto o cálculo integral surgiu de um problema aparentemente não relacionado, o problema da área. O mentor de Newton em Cambridge, Isaac Barrow (1630-1677), descobriu que esses dois problemas estão, na verdade, estreitamente relacionados. Ele percebeu que a derivação e a integração são processos inversos. O Teorema Fundamental do Cálculo dá a relação inversa precisa entre a derivada e a integral. Foram Newton e Leibniz que exploraram essa relação e usaram-na para desenvolver o cálculo como um método matemático sistemático. Considerando o contexto apresentado e seu conhecimento sobre integrais indefinidas assinale a alternativa correta na qual apresenta o processo para a solução da integral.
ATIVIDADE RESOLVIDA
R$15,00 NO PIX
75992709085 [NÚMERO DE TELEFONE]
R$15,00 CARTÃO DE CRÉDITO

APÓS FAZER O PAGAMENTO ACESSE O LINK ABAIXO
Contatos












Nenhum comentário:
Postar um comentário
Dúvidas? Sugestões? Fale com o Professor Carlão!